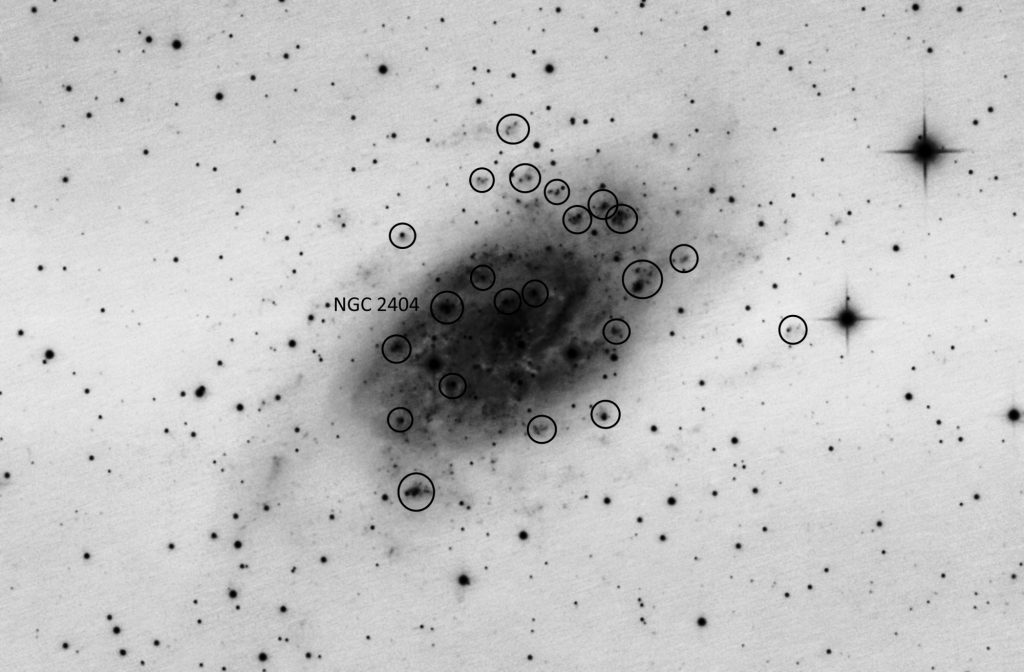
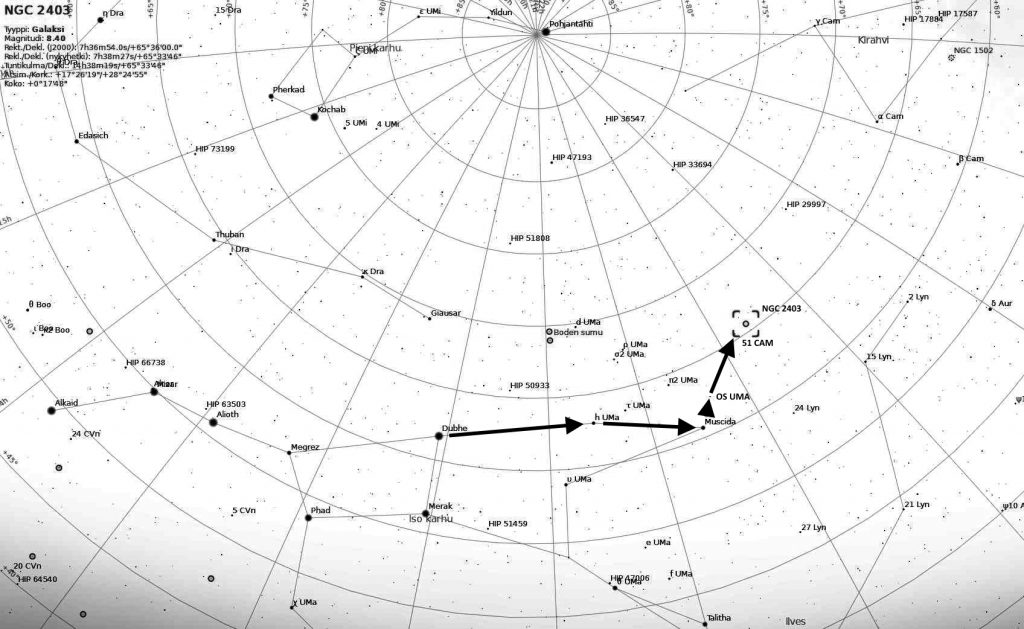
Kun yöllä katsoo taivaalle, voi pimeällä paikalla nähdä valtavasti tähtiä. Harvemmin kuitenkaan tulee ajatelleeksi, että vielä enemmän tähtiä me emme näe. Miltä taivas näyttäisi, jos näkisimme tähdet niiden kirkkauden sijaan sen mukaan, kuinka kaukana ne ovat meistä?
Oma aurinkokuntamme asustaa Linnunrata-galaksin kierteishaaran laidalla. Lähin naapurimme Alpha Kentauri on meistä runsaan 4 valovuoden päässä. Alpha Kentauri on kolminkertainen tähtijärjestelmä, jossa on kaksi kirkkaampaa tähteä sekä hyvin himmeä Proxima Kentauri. Alle kymmenen valovuoden päässä meistä on näiden lisäksi Barnardin tähti, Luhman 16, WISE 0855-0714, Wolf 359, Lalande 21185, Sirius, Luyten 726-8 sekä Ross 154. Vähänkin normaaleja tähtikarttoja tutkineelle nimet kuulostavat todella oudoilta. Näistä tähdistä Alpha Kentaurin lisäksi vain Sirius näkyy paljaalla silmällä.
Tähdet jaetaan spektriluokkiin niiden pintalämpötilan perusteella. Lämpötila taas johtuu tähden massasta, joka määrittyy tähden tiivistyessä tähtisumusta elämänsä alussa. Pääasiallisia spektriluokkia ovat O, B, A, F, G, K, M. Ensimmäiset kaksi (O ja B) ovat varsinkin O:n päässä todella kirkkaita ja massiivisia tähtiä, A, F, G ja K ovat keskikokoisia (kuten Aurinko, G-luokan tähti) ja M-luokan tähdet ovat pieniä punaisia kääpiöitä. (Koska spektriluokka määrittyy pintalämpötilan perusteella, voi M-luokan tähti olla myös valtava punainen jättiläinen, kuten Betelgeuse, mutta tässä artikkelissa puhutaan punaisista kääpiötähdistä.)
Punaiset kääpiöt ovat todella himmeitä, emmekä pysty näkemään niitä paljaalla silmällä. Jopa lähimmän aurinkokunnan ulkopuolisen tähden, Proxima Kentaurin, näkemiseen tarvitaan kaukoputki. Ja se ei ole yksin: Alle 10 valovuoden etäisyydellä olevista tähdistä myös Barnardin tähti, Wolf 359, Lalande 21185, Luyten 726-8 ja Ross 154 ovat punaisia M-luokan kääpiötähtiä. Niitä ei näe paljaalla silmällä, mutta ne ovat siellä. Tutkijat arvioivat, että n. 75% maailmankaikkeuden tähdistä on näitä himmeitä punaisia kääpiöitä! Me emme siis näe 3/4:aa tähdistä edes omassa ympäristössämme.
Sitten on vielä tähtiä, jotka eivät ole tähtiä ollenkaan. Kun tähtialkiot tiivistyvät tähtienvälisissä kaasupilvissä (siis tähtisumuissa), niiden lämpötila nousee. Jos lämpötila ja sisäinen paine ylittävät tietyn rajan, syttyy kappaleen sisällä ydinfuusio, ja tähti syttyy loistamaan. Maailmankaikkeudessa on kuitenkin valtavasti kappaleita, jotka jäävät riman alle. Tähtisumu kyllä tiivistyy alkioksi, mutta paine ja lämpötila ei riitä, ja fuusio ei koskaan ala. Koska nimenomaan fuusio on tähden määrittävä tekijä, eivät nämä epäonnistuneet tähdet ole tähtiä, vaan ruskeita kääpiöitä. Ne eivät ole planeettoja, koska ne eivät välttämättä kierrä mitään tähteä, ja ne voivat olla pienten tähtien kokoisia. Koska ne säteilevät lähinnä infrapunataajuuksilla, niitä on todella vaikea havaita. (Maan ilmakehä absorboi paljon infrapunasäteilyä, joten tarvitaan avaruuskaukoputki. Juuri sopiva on esimerkiksi James Webb Space Telescope.) Ensimmäiset ruskeat kääpiöt löydettiin 1990-luvun puolivälissä. Raja punaisten ja ruskeiden kääpiöiden välillä on joskus kuitenkin hyvin häilyvä.
Millainen olisi tähtikartta, jos sen laatisi tähtien etäisyyden perusteella? Oheinen kartta sen näyttää. Siinä näkyvät aurinkokunnan lähinaapurit 30 valovuoden säteellä. Mitä suurempi tähti, sen lähempänä se on meitä. Pikavilkaisulla huomaa, että kartta on punaisten pisteiden täyttämä. Punaisia kääpiöitä siis riittää! Kunnollisia nimiä niillä ei ole, vaan lähinnä erilaisten luetteloiden numeroita. Vielä karumpia ovat ruskeiden kääpiöiden nimitykset, joissa on yleensä mukana myös niiden koordinaatit.
Muutamia kirkkaampia tähtiä mahtuu kuitenkin joukkoon. Tutuin lienee Sirius, tähtitaivaan kirkkain tähti, joka on vajaan yhdeksän valovuoden päässä meistä. Myös Altair, Vega ja Procyon mahtuvat karttaan, ne ovat siis alle 30 valovuoden päässä. Myös himmeämpiä paljaan silmän tähtiä löytyy, kuten Sigma Draconis tai Eta Cassiopeiae. Kaikki paljaalla silmällä näkyvät ovat maltillisia keskikokoisia tähtiä, yhtään O tai B -luokkien tähtiä lähietäisyydellämme ei ole.
Karttaa kannattaa tutkia myös kolmiulotteisuus mielessä. Tähtien koot kertovat niiden etäisyydestä. Epsilon Eridani ja 40 Eridani ovat melko lähellä toisiaan samassa suunnassa. Miltä 40 Eridani mahtaisi näyttää Epsilonin taivaalla? Millaisia järjestelmiä kaksois- tai useampikertaiset ovat? (Tässä kartassa kaksoistähdet on määritetty niiden kirkkaamman komponentin mukaan.)
Universumissamme on niin paljon sellaista, jota emme näe! Iloista tutkimista!
Kartan laati ja artikkelin kirjoitti Eeva-Kaisa Ahlamo






 Star Wars eli Tähtien sota toi ihmisten tietoisuuteen Voiman, salaperäisen energiakentän, jota jediritarit hyödyntävät toimissaan. Mikä tämä voima oikeastaan on? Mitkä säännöt sitä ohjaavat? Tässä esseessä selvitellään kvanttifysiikan kautta sitä, mitä Voimasta tiedetään.
Star Wars eli Tähtien sota toi ihmisten tietoisuuteen Voiman, salaperäisen energiakentän, jota jediritarit hyödyntävät toimissaan. Mikä tämä voima oikeastaan on? Mitkä säännöt sitä ohjaavat? Tässä esseessä selvitellään kvanttifysiikan kautta sitä, mitä Voimasta tiedetään.